
1、题目名称
Rectangle Area(矩形交叉部分的面积)
2、题目地址
3、题目内容
英文:Find the total area covered by two rectilinear rectangles in a 2D plane. Each rectangle is defined by its bottom left corner and top right corner as shown in the figure.
中文:在一个2维平面中给出两个矩形的左下角和右上角坐标,求这两个矩形交叉部分的面积。
例如下图中,给出A、B、C、D、E、F、G、H四个数字,交叉部分面积为2*3=6

4、解题方法1
各点坐标换算后,两个矩形的四角坐标如下图所示:
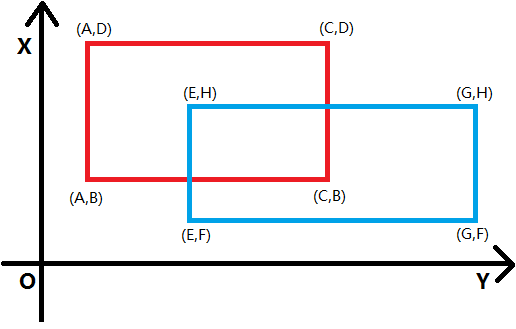
可以看出,两个矩形交叉的部分(如果有)也是一个矩形,只需要知道交叉部分矩形的长和宽,就可以求出交叉部分的面积了。给出的8个数字是两个矩形左下角、右上角共计4个点的坐标,可以用它们求出交叉部分矩形的长和宽。
/** * 功能说明:LeetCode 223 - Rectangle Area * 开发人员:Tsybius2014 * 开发时间:2015年8月28日 */public class Solution { /** * 计算矩形面积 * @param A 矩形1的左下角横坐标(矩形1左边横坐标) * @param B 矩形1的左下角纵坐标(矩形1下边纵坐标) * @param C 矩形1的右上角横坐标(矩形1右边横坐标) * @param D 矩形1的右上角纵坐标(矩形1上边纵坐标) * @param E 矩形2的左下角横坐标(矩形2左边横坐标) * @param F 矩形2的左下角纵坐标(矩形2下边纵坐标) * @param G 矩形2的右上角横坐标(矩形2右边横坐标) * @param H 矩形2的右上角纵坐标(矩形2上边纵坐标) * @return 交叉区域面积 */ public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) { //内部交叉区域(如果有)的四个边界 int innerLeft = A > E ? A : E; int innerRight = C < G ? C : G; int innerTop = D < H ? D : H; int innerBottom = B > F ? B : F; //计算内部交叉区域面积,要考虑两个矩形可能不相交的情况 int innerWidth = innerTop > innerBottom ? (innerTop - innerBottom) : 0; int innerHeight = innerRight > innerLeft ? (innerRight - innerLeft) : 0; int innerArea = innerWidth * innerHeight; return (C - A) * (D - B) + (G - E) * (H - F) - innerArea; }} 5、解题方法2
如果想不到上面那种比较简单的方法,那就只能硬着头皮用if语句一个一个穷举情况了。穷举的基本思路是:
1)矩形1在矩形2内的情况
2)矩形2在矩形1内的情况
3)矩形1、2无交叉的情况
4)矩形1有一边嵌入矩形2的情况(4种)
5)矩形2有一边嵌入矩形1的情况(4种)
6)矩形1和矩形2有一个角相交的情况(4种)
7)矩形1和矩形2组成一个十字形的情况(2种)
这种方法的缺点是,条件不容易穷举全,在写的时候非常容易出错,因此非常考验写代码人考虑问题思维的严谨性。
一段实现此穷举方法的Java代码如下:
/** * 功能说明:LeetCode 223 - Rectangle Area * 开发人员:Tsybius2014 * 开发时间:2015年9月1日 */public class Solution { /** * 计算矩形面积 * @param A 矩形1的左下角横坐标 * @param B 矩形1的左下角纵坐标 * @param C 矩形1的右上角横坐标 * @param D 矩形1的右上角纵坐标 * @param E 矩形2的左下角横坐标 * @param F 矩形2的左下角纵坐标 * @param G 矩形2的右上角横坐标 * @param H 矩形2的右上角纵坐标 * @return 交叉区域面积 */ public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) { //矩形1和矩形2的面积 int area1 = (C - A) * (D - B); System.out.println("Area1:" + area1); int area2 = (G - E) * (H - F); System.out.println("Area2:" + area2); //矩形2在矩形1内的情况 if (A <= E && B <= F && C >= G && D >= H) { return area1; } //矩形1在矩形2内的情况 if (A >= E && B >= F && C <= G && D <= H) { return area2; } //矩形1与矩形2无交集的情况 if (A >= G || B >= H || C <= E || D <= F) { return area1 + area2; } //交叉区域面积 int areaDelta = 0; //矩形1在矩形2有交集且矩形2上嵌于矩形1的情况 if (A <= E && C >= G && B <= F && D <= H) { areaDelta = (G - E) * (D - F); } //矩形1在矩形2有交集且矩形2下嵌于矩形1的情况 else if (A <= E && C >= G && B >= F && D >= H) { areaDelta = (G - E) * (H - B); } //矩形1在矩形2有交集且矩形2左嵌于矩形1的情况 else if (B <= F && D >= H && A >= E && C >= G) { areaDelta = (H - F) * (G - A); } //矩形1在矩形2有交集且矩形2右嵌于矩形1的情况 else if (B <= F && D >= H && A <= E && C <= G) { areaDelta = (H - F) * (C - E); } //矩形1在矩形2有交集且矩形1上嵌于矩形2的情况 else if (E <= A && G >= C && F <= B && H <= D) { areaDelta = (C - A) * (H - B); } //矩形1在矩形2有交集且矩形1下嵌于矩形2的情况 else if (E <= A && G >= C && F >= B && H >= D) { areaDelta = (C - A) * (D - F); } //矩形1在矩形2有交集且矩形1左嵌于矩形2的情况 else if (B >= F && D <= H && C <= G && A <= E) { areaDelta = (D - B) * (C - E); } //矩形1在矩形2有交集且矩形1右嵌于矩形2的情况 else if (B >= F && D <= H && C >= G && A >= E) { areaDelta = (D - B) * (G - A); } //矩形1与矩形2有交集且矩形2在左上 else if (A > E && B < F && C > G && D < H) { areaDelta = (G - A) * (D - F); } //矩形1与矩形2有交集且矩形2在左下 else if (A > E && B > F && C > G && D > H) { areaDelta = (G - A) * (H - B); } //矩形1与矩形2有交集且矩形2在右上 else if (A < E && B < F && C < G && D < H) { areaDelta = (C - E) * (D - F); } //矩形1与矩形2有交集且矩形2在右下 else if (A < E && B > F && C < G && D > H) { areaDelta = (E - C) * (B - H); } //矩形1与矩形2交叉后呈十字,矩形1为横线 else if (A < E && C > G && B > F && D < H) { areaDelta = (D - B) * (G - E); } //矩形1与矩形2交叉后呈十字,矩形1为竖线 else if (A > E && C < G && B < F && D > H) { areaDelta = (C - A) * (H - F); } //System.out.println("AreaDelta:" + areaDelta); //System.out.println("Result:" + (area1 + area2 - areaDelta)); return area1 + area2 - areaDelta; }} END